Gaussian mixture model (GMM), Clustering The next best alternative to overcome the limitations of Kmeans

Hi everyone, how are you doing? likewise today I will introduce you to one of the powerful algorithms/models to clustering called Gaussian Mixture Models (GMM) in short. But before that let’s first understand why GMM is the next best clustering model by comparing it with Kmeans.
Kmeans:
Kmeans uses an iterative approach known as expectation-maximization. EM in short. The process of EM includes
- Randomly assign some cluster centers
- Repeat steps 3 and 4 until it further cant be converged.
- E-Step: assign points to the nearest cluster center
- M-Step: set the cluster centers to the mean
In simple words:
- Determine the K value by elbow method & assign K ( the number of clusters)
- Randomly assign each data points to a cluster
- Determine the cluster centroids
- Determine the distance of each data point to the centroids and reassign each point to the closest cluster centroid based upon minimum distance.
- Calculate cluster centroids again.
- Repeat steps 4 & 5 until we reach the global optima where no improvements are possible
Common drawbacks:
Kmeans might perform slowly for a large dataset. Because each iteration of the Kmeans must access every point in the dataset, thus the algorithm will be relatively slow with the increase in the number of sample data.
One of the major drawbacks of Kmeans, the number of clusters must be selected beforehand. This is a common challenge because Kmeans cannot learn the number of clusters from the data.
However, i have fixed the issue of determining the number of clusters K for Kmeans, check out my article autoelbow or visit pypi.org and search autoeblow
Moving ahead let's get into brief of
What is Expectation-Maximization?
EM i.e. Expectation- Maximization is a statistical algorithm for finding the right model parameters. We typically use EM when the data have missing values, in other words, the data is incomplete.
These missing values/variables are called latent variables.
EM tries to use the existing data to determine the optimum values for these variables and then finds the model parameters and based on these model parameters we update the values for the latent variable.
it includes 2 step E-Step: the available data is used to estimate(guess) the values of the latent values and the M-Step on the estimated values from the E-step updates the parameters.
Expectation-Maximization is the based of many algorithm including Gaussian Mixture Models and Kmeans
There are tons of articles based on the algorithmic way to understand the E and M step of the Expectation-Maximization.
Let’s get into the hands-on with the GM models to find the clusters
A Gaussian mixture model (GMM) attempts to find a mixture of multidimensional Gaussian probability distributions. and because GMM contains a probabilistic model it is possible to find the probability of the given cluster belongs to.
GMM helps to overcome the lack of flexibility in the cluster shape of Kmeans which we will see later during the course and also overcomes the lack of probabilistic cluster assignment.
However, GMM is a bit difficult to interpret the results.
K-Means primarily uses 2 parameters: the number of clusters K and the centroids and GMM uses 3 parameters: the number of clusters K, mean, and the cluster covariances.
#create a dummy dataset
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1] # flip axes for better plotting
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
Before we apply GMM, create a user-defined plot function that will help us to understand the shape of the cluster by GMM and Kmeans
#Gmm
from matplotlib.patches import Ellipse
def plot_gmm(gmm, X, label=True, ax=None):
def draw_ellipse(position, covariance, ax=None, **kwargs):
ax = ax or plt.gca()
if covariance.shape == (2, 2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
for nsig in range(1, 4):
ax.add_patch(Ellipse(
position, nsig * width, nsig * height,
angle, **kwargs
))
ax = ax or plt.gca()
labels = gmm.fit(X).predict(X)
if label:
ax.scatter(X[:, 0], X[:, 1], c=labels, s=7, cmap='viridis', zorder=2)
else:
ax.scatter(X[:, 0], X[:, 1], s=7, zorder=2)
ax.axis('equal')
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(pos, covar, alpha=w * w_factor)
#keams
from scipy.spatial.distance import cdist
def plot_kmeans(kmeans, X, ax=None):
labels = kmeans.fit_predict(X)
# plot the input data
plt.figure(dpi=175)
ax = ax or plt.gca()
ax.axis('equal')
ax.scatter(X[:, 0], X[:, 1], c=labels, s=7, cmap='viridis', zorder=2)
# plot the representation of the k-means model
centers = kmeans.cluster_centers_
radii = [
cdist(X[labels == i], [center]).max()
for i, center in enumerate(centers)
]
for c, r in zip(centers, radii):
ax.add_patch(plt.Circle(
c, r, fc='#DDDDDD', lw=3, alpha=0.5, zorder=1
))
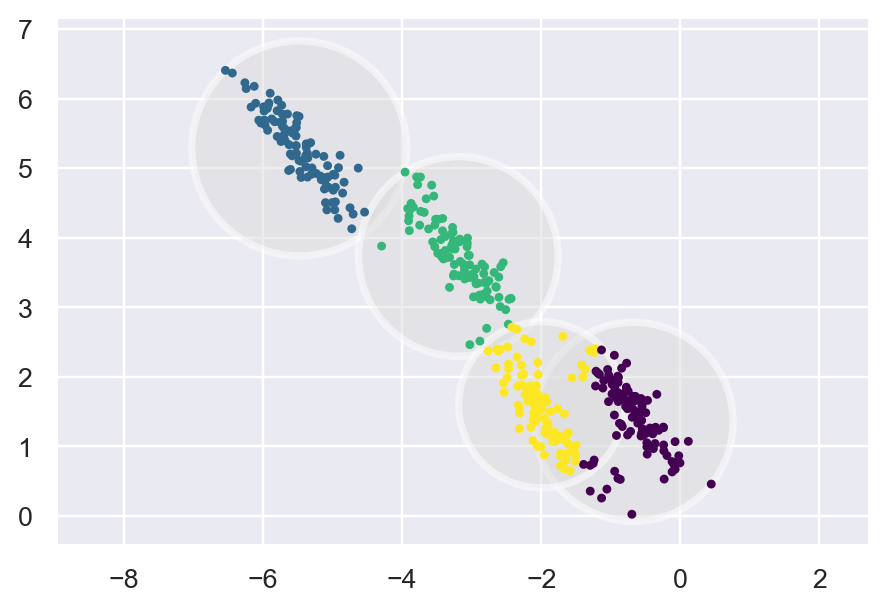
Kmeans
kmeans = KMeans(n_clusters=4, random_state=0).fit(X_stretched)
labels_knn = kmeans.predict(X_stretched)
plot_kmeans(kmeans, X_stretched)
GMM
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=4, covariance_type='full', random_state=42).fit(X_stretched)
labels_gmm = gmm.predict(X_stretched)
plt.figure(dpi=175)
plot_gmm(gmm, X_stretched)
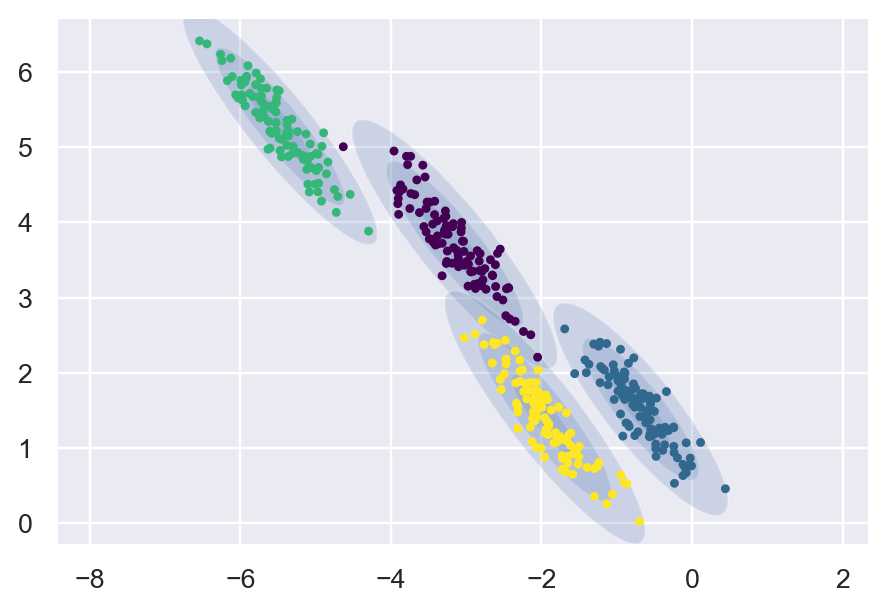
We can clearly notice the shape of Kmeans and the shape of GMM. Kmeans are restricted to a Circular shape.
Since GMM is a probabilistic model we can also get the probabilities using
probabilities = gmm.predict_proba(X_stretched)
probabilities
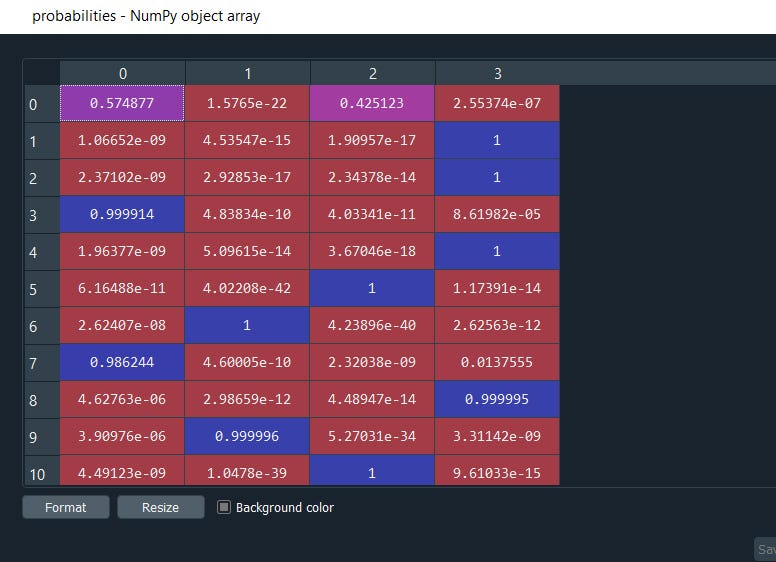
Here we are, all 4 clusters along with their probabilities. This is very helpful and gives the flexibility to filter out the results based on a threshold.
That's it, Congratulations we now perform GMM as the next best alternatives to Kmeans, i hope you enjoyed it.
If you like to know more about advanced types of clustering follow my other article A-Z Clustering
Some of my alternative internet presences are Facebook, Instagram, Udemy, Blogger, Issuu, and more.
Also available on Quora @ https://www.quora.com/profile/Rupak-Bob-Roy
Have a good day. Talk Soon.

Comments
Post a Comment